What is the bias in a Javascript neuronal network?

Machine learning works by estimating functions. So, let's say we have a function represented by the following graph:

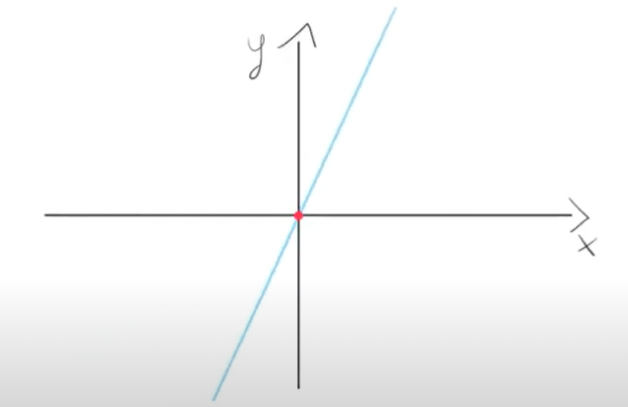
This function can be defined by a formula like f(i) = i * w, or by this Javascript code:

const f = (x) => x*w

From a neuronal network point of view, this means that we have an input neuron with a weight and an output neuron. The output will be the product of the input and the weight:

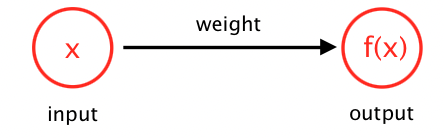
During the training phase of the neuronal network, we will determine the needed weight to apply to the input so that it will produce the expected output.

But, what if the graph of the function looks like this:

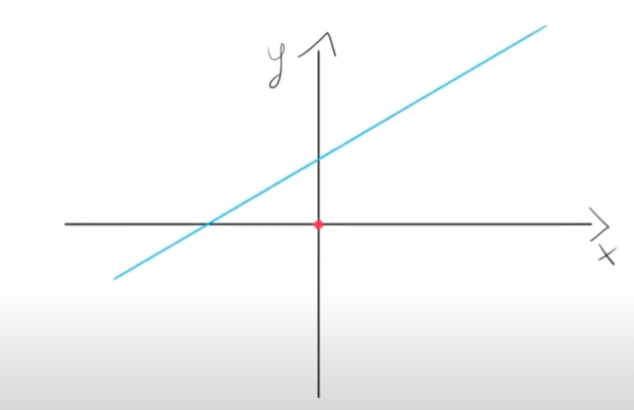
Then the previous neuronal network will not work, as it can only estimate functions that pass through the origin [0,0] point, because if the input x is zero then f(x) will be zero.

A more appropriate way to estimate that function is by using a formula such as f(x) = x * w + b, or to put it in Javascript:

const f = (x) => x*w + b

The b variable is called a bias. Adding this b variable is exactly what is needed so that we can produce function estimations where f(0) is not zero.

The bias is trainable, meaning that it changes values during the training phase of the neuronal network, as the weights do.

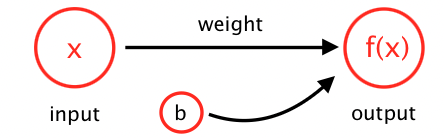
Therefore we can say that a bias is a value that will be added to the weighted sum of the inputs and weights so that it can adjust the output. The bias value allows us to shift the activation function to either left or right, allowing us to get access to more flexible models.

---